肿瘤研究的显著性水平和检验效能该如何设置? 除非在探索最大耐受剂量(MTD)的基础上扩大研究队列并进行假设检验,否则显著性水平一般不适用于I期研究。 2肿瘤研究的分析集该如何定义? 全分析集(Full Analysis Set, FAS)通常定义为所有接受随机的受试者(随机试验),或所有入组/使用药物的受试者(非随机试验)。 符合方案集(Per Protocol Analysis Set, PPS)是全分析集的子集,会在FAS基础上剔除一些满足某些条件的受试者,这些条件往往与研究终点、试验设计或入排标准有关,并且需要在SAP中有所定义。 最后介绍一下划分数据集时经常提到的方案偏离。注意区分方案偏离和方案违背,方案违背是严重程度较高的方案偏离。对方案偏离的判断,主要基于入排标准以及其他一些方案中规定的流程标准。所有影响受试者安全性、研究执行或结果评价的方案偏离都需要报告,包括但不限于: 纳入不满足入排标准的受试者并给药 受试者接受错误的治疗或错误的剂量 受试者使用了方案禁止的合并用药 违反GCP 由于关于MTD集的相关介绍文章较少,这里举一个MTD集相关的方案偏离例子,通常MTD集需要剔除在DLT评估期发生重大治疗偏倚的受试者,包括但不限于: DLT评估期真实使用的用药总量比计划使用的总量少x%(假设不是由于出现DLT退出试验造成的) DLT评估期真实使用的用药总量比计划使用的总量多x% 联合治疗中,某种研究药物未使用(设不是由于出现DLT退出试验造成的) 某些方案中规定在给药前需要进行的预防措施未执行 我们可以通过以下三种情况介绍一下通常的做法: 随机后未给药,根据SS的定义,出现该情况的受试者是不会被纳入SS分析的,亦不会被纳入PK分析集,但是根据FAS定义,该受试者会被纳入分析集并按照所随机分配的治疗组进行统计分析。在PPS中,该受试者一般会被剔除。 随机后给药,但是给错了研究药物,除了PPS,出现该情况的受试者一般会被纳入分析集,但是不同分析集统计分析的处理方法不同。对于SS和PK集,受试者一般会按照所随机分配的治疗组进行统计分析,除非是全部或超过xx%的给药给错,具体xx%需要根据不同试验而定。对于FAS,通常会归类到所随机分配的组下。 未随机,但是给予了研究药物,出现该情况的受试者由于未随机,一般不会被纳入到FAS和PPS,但是会按照实际治疗分组,进入SS和PK分析集。 期中分析主要分哪些情况? (1)以反应率为终点指标的II期单臂研究 这类II期研究设计的期中分析,往往用以判断试验药是否无效的,而不是用于判断药物有效而提前终止,但是从开展后续III期研究的角度考虑,也可能会进行事先商议有效性的标准 (这些内容可能不会包含在方案里)。根据不同试验情况,可以进行一次或多次期中分析。以一次期中分析为例,在第一阶段入组结束并达到分析要求(如最后一例受试者完成两次疗效评估)时,将会进行一次正式的期中分析,用以判断药物是否无效,以及试验是否该继续入组第二阶段受试者。如果在进行期中分析前,试验已经满足进入第二阶段的标准,则可以直接入组第二阶段受试者,否则入组进程会在第一阶段入组完成后暂停,等待期中分析结果而决定是否需要继续。如果分析结果不满足继续进行试验的标准,则试验终止。注意,单臂试验往往以反应率为主要终点,如ORR,而不推荐看OS和PFS这类指标。 此类单臂设计,根据研究不同目的,主要有如下几种选择: 目前较多采用的方法为Simon’s Two Stage设计[2],主要包括了Optimal和Minimax两种方法,Optimal平均期望样本量(EN)最小,而Minimax总样本量最小,即Optimal在期中分析时需要的样本量小于Minimax,但是需要的总样本量大于Minimax。从下表可以看到,Minimax第一阶段需要22例受试者,而Optimal只需要13例受试者。但是,Minimax的总样本量和只做一次分析的单阶段设计一致,而Optimal设计的总样本量要多14例,达到55例。所以在两者平均期望样本量相差不大(27.08 VS 23.51)的情况下,Minimax总样本量少很多,但是Optimal能在更少的样本量下给出一个Stage One结论,即如果药物无效,Optimal可以更早的停止试验,以免更多受试者暴露于无效治疗中。 表1. 不同方法二阶段设计样本量比较 (P0=0.2, p1=0.4, Alpha=0.025(单侧),Beta=0.200) 分层分析和亚组分析该怎么做? 参考文献
针对II期研究,如果考虑使用假设检验,可以对I类和II类错误设定更加宽松的显著性水平,例如α可以超过0.05(双侧),使用0.1(双侧),此外II期研究中也经常考虑使用贝叶斯相关的方法。
对于平行对照的III期研究,总体I类错误一般控制在单侧0.025或双侧0.05以内,检验效能一般设为90%。
需要注意的是:任何以注册申报为目的的试验,在设计阶段都应该考虑设置适当的I类和II类错误。如果进行多重比较,需要确保总体I类错误控制在单侧0.025或双侧0.05以内。
安全集(Safety Analysis Set, SS)一般定义为所有至少使用过一次研究药物的受试者。注意,如果1例使用过药物的受试者,其某一安全性指标,如ECG没有基线后数据,或在做相对基线变化时缺少基线数据,那么该受试者会纳入安全集,但是其缺失数据的安全性指标ECG将不会进行统计分析。关于上述情况的处理方法,与现在很多国内申办方方案中的SS定义:所有至少使用过一次研究药物,且至少有一次用药后安全性评价的受试者,两者在数据集上的划分处理方法是不一样的,要注意加以区分,推荐使用本段标记为绿色的定义和做法。
其他分析集,包括MTD分析集,PK浓度分析集,PK参数分析集,PD分析集,Biomarker分析集等等,统计师可以和医学讨论根据需要添加分析人群,比如肿瘤试验中对照组进展后会专组接受试验药物,所以可以定义一个交叉治疗分析集,诸如此类。某些疗效终点如PRO(Patient Reported Outcome)由于需要分析相对基线变化,所以可以不基于FAS,而单独定义一个PRO分析集,比如可以定义为:FAS的子集,所有有基线和至少一次随访PRO评估的受试者。
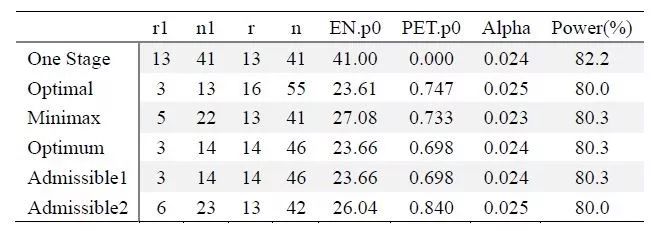
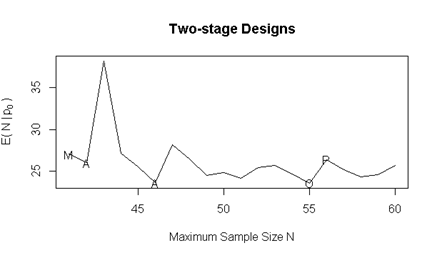
(2)随机对照II期研究
除了单臂试验,II期研究当然也可以按随机对照试验开展,相比单臂试验,随机对照试验可以减小偏倚,亦可以OS或PFS作为主要研究终点。和单臂II试验一样,随机对照II期试验一般亦是无效终止,如果期中分析的结果未能拒绝预先设定的无效终止界值,试验将因无效而终止。对于以时间-时间为终点的II期 Two Stage 设计统计学方法,可以参考Jung[13]的文章。
(3)以时间-事件为终点指标的III期研究
这种情况是目前三期肿瘤试验期中分析遇到最多的情况,如果要全部讲清楚,篇幅会非常长,所以这里只讲一些基本原则,更具体的之后会有文章单独介绍。在观察到规定的事件数,规定的信息比或规定的研究时长后,试验将按计划开展期中分析,期中分析的数量一般不超过3次,虽然使用O’Brien-Fleming-type cumulative error spending(注意不是O’Brien-Fleming method)等方法可以在任意时间进行期中分析,但是还是推荐按事先计划进行,尽量避免计划外的期中分析。针对主要终点指标的期中分析,界值的设定一般都很保守(只有疗效结果出现统计学上很显著的差异才会终止试验)。不过期中分析也可能会针对次要终点指标进行(例如当OS是主要终点指标时,针对PFS进行分析)。每次期中分析时的试验终止界值和检验水准互相对应,双侧检验的终止边界对称,而单侧检验的终止边界则需要根据有效终止和无效终止两种情况共同确定。
无论是双侧检验还是优效或非劣效的单侧检验,统计分析时Log-rank和分层Log-rank检验都是标准的检验方法。由于期中分析的存在,最终分析时的检验水准需要进行校正,以使总体I型错误与常规设定(单侧0.025或双侧0.05)保持一致。经典的期中和最终有效性检验采用Lan-DeMets α消耗函数的O’Brien-Fleming界值。针对无效终止分析的β消耗函数,可以被作为非强制性边界,但不应该设定过于严苛的边界,或者可以使用条件检验效能(conditional power),代替β消耗的方法分析试验成功或失败的可能性。期中分析的主要统计学设计应在方案定稿阶段确定,统计分析计划可以提供更加详细的说明。期中分析较常用的软件是SAS和EAST,当然也有很多相应的R package,或者可以自己根据原理写R程序。
(4)样本量重估计
期中分析样本量重估计需要考虑的一个关键因素就是期中分析时数据的成熟度,如果期中分析时删失数据过多,将很可能无法提供一个可参考的样本量重估计结果。
定性或定量终点的样本量重估计通常可以基于期中分析的δ(疗效)和σ(标准差)调整,但是由于时间-事件终点的特殊性,肿瘤研究时间-事件终点多以根据期中分析揭盲后的疗效信息进行样本量重估计。所以如果期中分析观察到的治疗效果小于预期但仍具有临床意义,我们可以根据之前研究获得的非盲疗效信息,进行样本量重估计。样本量重估计在应用上一般只考虑增加样本量而不考虑减少样本量。在样本量重估计的方法上,主要包括基于条件效能(conditional power)和预测效能(predictive power)两种,CHW[14]是一个比较经典的方法,该方法在序贯设计(Group sequential design)的框架下控制了适应性设计的I型错误,样本量随(非盲)数据变化而变化,并且可应用于时间-事件终点指标。有兴趣也可以去读一下Pocock[15]的这篇文章,里面有一些具体操作层面的考量和例子,比如样本量最大可以增大到多少该如何决定等等。关于时间-事件终点在盲态下的样本量重估计,相关参考文献较少,这里列出一篇通过EM迭代估算的方法[16]。
值得注意的是,设计缺陷以及研究执行层面所造成的偏倚,也会因样本量的增加而被放大[17]。因此,在研究设计阶段,通过计算机模拟各种场景下的结果,并前瞻性地计划好样本量重估计执行过程是非常重要的,只有这样,才能将研究过程中相关的统计和执行偏倚最小化,从而减小偏倚对治疗效果估计以及研究结果解释的影响。此外在注册试验中,样本重估计的方案需要和监管机构沟通并得到认可。
(5)期中分析结果发布
在盲态试验中,期中分析的揭盲后统计结果一般只有DMC成员才能看到,而项目组成员一般只有在锁库揭盲后的最终分析才能看到结果。无论主要还是次要疗效终点都应该按照上述原则执行。关于DMC的建立和执行可以参考ICH相关指导原则Guidance for Clinical Trial Sponsors Establishment and Operation of Clinical Trial Data Monitoring Committees [18],关于DMC中常见的问题,以及独立统计师所扮演的角色,可以参考Fleming[19]和De Mets[20]的文章。
[2] Richard Simon, Optimal Two-Stage Designs for Phase II Clinical Trials, Clinical Trial. Control Clin Trials, 1989, 10:1-10.
[3]Sin-Ho Jung, SL. George, et.al, Admissible two-stage designs for phase II cancer clinical trials, Statist. Med. 2004; 23:561–569
[4] Jung SH, Carey M, Kim KM. Graphical search for two-stage designs for phase II clinical trials. Controlled Clinical Trials 2001; 22:367–372.
[5] Ensign LG, Gehan EA, Kamen DS. An optimal three-stage design for phase II clinical trials. Stat Med, 1994, 13: 1727-1736.
[6] Chen T.T, Optimal three-stage designs for phase II cancer clinical trials. Stat Med, 1997, 16: 2701-2711.
[7] J Jack Lee, Diane D Liu, A predictive probability design for phase II cancer clinical trials, Clinical Trials 2008; 5: 93–106.[8] Y. Lin and W.J. Shih (2004), Adaptive Two-Stage Designs for Single-Arm Phase IIA Cancer Clinical Trials, Biometrics 2004, 60: 482-490.
[9] Adrienne Groulx, Kyung-hee (Kelly) Moon, et.al. Using SAS® to Determine Sample Sizes for Traditional 2-Stage and Adaptive 2-Stage Phase II Cancer Clinical Trial Designs, SAS Global Forum 2007, Paper 188.
[10] S.G. Thompson, A.P. Mander, Two-stage designs optimal under the alternative hypothesis for phase II cancer clinical trials, Clinical Trials 2010, 31: 572–578
[11] Fleming TR. One-sample Multiple Testing Procedure for Phase II Clinical Trials. Biometrics, 1982, 38: 143-151
[12] Gehan EA, The determination of the number of patients required in a follow-up trial of a new chemotherapeutic agent. J Chron Dis 1961, 13:346-353
[13] Sin-Ho Jung, Minjung Kwak, Optimal two-stage log-rank test for randomized phase II clinical trials, Journal of Biopharmaceutical Statistics 2016: 1-20.
[14] Cui L, Hung HMJ, Wang S, et al. Modification of sample size in group-sequential clinical trials. Biometrics. 55: 853-7, 1999.
[15] Mehta C R , Pocock S J . Adaptive Increase in Sample Size When Interim Results are Promising: A Practical Guide With Examples[J]. Statistics in Medicine, 2011, 30(28):3267-3284.
[16] Huang L , Bai J , Yu H , et al. Sample size re-estimation without un-blinding for time-to-event outcomes in oncology clinical trials[J]. The Journal of Biomedical Research, 2018(1):23-29.
[17] Food and Drug Administration (FDA). Draft Guidance for Industry: Adaptive Design Clinical Trials for Drugs and Biologics, 2010.
[18] Guidance for Clinical Trial Sponsors Establishment and Operation of Clinical Trial Data Monitoring Committees, 2006
[19] Fleming T R , Ellenberg S S , Demets D L . Data Monitoring Committees: Current issues. Clinical Trials, 2018 Aug;15(4):321-328
[20] D De Met, The independent statistician model: How well is it working? Clin Trials. 2018 Aug;15(4):329-334
本网站所有内容来源注明为“梅斯医学”或“MedSci原创”的文字、图片和音视频资料,版权均属于梅斯医学所有。非经授权,任何媒体、网站或个人不得转载,授权转载时须注明来源为“梅斯医学”。其它来源的文章系转载文章,或“梅斯号”自媒体发布的文章,仅系出于传递更多信息之目的,本站仅负责审核内容合规,其内容不代表本站立场,本站不负责内容的准确性和版权。如果存在侵权、或不希望被转载的媒体或个人可与我们联系,我们将立即进行删除处理。
在此留言













#统计学#
69